题目

861. 翻转矩阵后的得分 - 力扣（LeetCode）

给你一个大小为 m x n 的二元矩阵 grid ，矩阵中每个元素的值为 0 或 1 。

一次 移动 是指选择任一行或列，并转换该行或列中的每一个值：将所有 0 都更改为 1，将所有 1 都更改为 0。

在做出任意次数的移动后，将该矩阵的每一行都按照二进制数来解释，矩阵的 得分 就是这些数字的总和。

在执行任意次 移动 后（含 0 次），返回可能的最高分数。

示例 1：

img

1
2
3
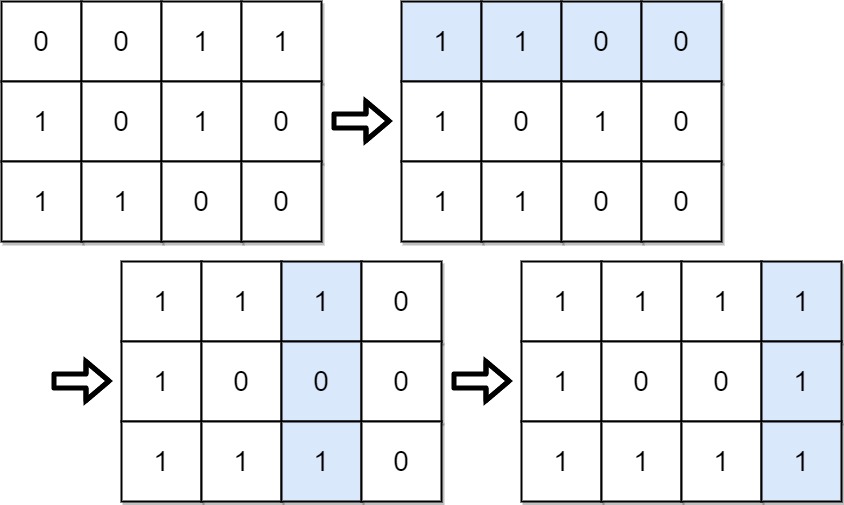
输入：grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
输出：39
解释：0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

示例 2：

1
2
输入：grid = [[0]]
输出：1

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 20
  • grid[i][j] 为 0 或 1

解题

这道题使用了贪心策略。

首先我们知道，矩阵有m行n列。这里我们设首列（最左边的列）是第0列。

贪心思路是这样的：

  • 将首列全部变为1（为了得到最高的分数）
  • 接着对于后续每一列，我们都让该列上1的数目尽可能的多（如果该列上0的数目多于1的数目，就翻转该列）

在实际编码时，我们是这样实现的：

  1. 首先，我们初始化结果变量ret为矩阵的行数m乘以2的n-1次方。因为我们首先将首列全部变为1嘛，而首列的权值是2^(n-1)。
  2. 接着，对于后续的每一列（从第一列开始遍历到最后一列）：
    1. 我们统计当前列中1的数量以及0的数量。
    2. 然后取两者中较大的值，我们设为k，k就是翻转后1的数量。
    3. 然后将k乘以2的n-j-1次方，再累加到ret变量即可。
  3. 最终将ret变量返回。

在计算每一列上1的数量时，我们是这么计算的：

  1. 如果首列的元素是1，直接加上当前列的值
  2. 如果首列的元素是0，则需要加上当前列值为0的元素个数（这是因为首列元素为0，则需要翻转该行将首列元素变为1。那么该行上为0的元素翻转后就是1了）。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int matrixScore(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;

        int ret = m * (1 << (n - 1));

        for(int j = 1; j<n; j++) {  // 遍历每一列 j
            int nOnes = 0;
            for(int i = 0; i<m; i++) {  // 遍历每一行 i
                if(grid[i][0] == 1) nOnes+= grid[i][j];
                else nOnes += (1 - grid[i][j]);
            }
            int k = Math.max(nOnes, m-nOnes);
            ret += k * (1<<(n-j-1));
        }

        return ret;
    }
}