二叉树的遍历
遍历是数据结构中的常见操作(访问数据结构中的所有元素)。
线性数据结构的遍历比较简单,正序遍历或逆序遍历。而对于二叉树来讲,根据节点访问顺序的不同,可以分为四种:
- 前序遍历(Preorder Traversal)
- 中序遍历(Inorder Traversal)
- 后序遍历(Postorder Traversal)
- 层序遍历(Level Order Traversal)
下面我们来看看他们的特点。
前序遍历(Pre-Order Traversal)
前序遍历二叉树,就是先访问根结点(中间节点),再前序遍历左子树,最后前序遍历右子树。

如上图:
我们再回想一下,前序遍历的访问顺序是什么?首先根节点肯定是最先被访问,然后是左子树,最后才是右子树。
因此在上图中,前序遍历的访问顺序如下:
- 访问根节点 F
- 访问左子树 B
- 访问右子树 G
前序遍历的顺序是 [F]->[B]->[A]->[D]->[C]->[E]->[G]->[I]->[H]。这表示在按照前序遍历方式访问树的时候,首先访问根节点 F,然后按照左子树和右子树的顺序递归进行访问。
由于树本身是一种递归定义的数据结构,因此很自然也可以用递归的方式来遍历。
用递归法对二叉树进行前序遍历:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode node, List<Integer> result) {
if (node == null) {
return;
}
result.add(node.val);
preorder(node.left, result);
preorder(node.right, result);
}
|
可以看到,递归的方式去前序遍历二叉树很简单,思路也很清晰。
如果使用迭代的方式实现前序遍历,可以使用栈数据结构来模拟递归的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if(root == null) return result;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode current = stack.pop();
result.add(current.val);
if(current.right != null) stack.push(current.right);
if(current.left != null) stack.push(current.left);
}
return result;
}
|
这个迭代的实现使用栈来模拟递归,首先将根节点(也就是中间节点)入栈,然后在循环中弹出当前节点,将其值添加到result中,并按照先右后左的顺序将右子树和左子树入栈。这样可以模拟前序遍历的顺序。
- Q:为什么要先加入右节点,再加入左节点呢?
- A:因为这样出栈的时候才是先左后右的顺序。
中序遍历(In-Order Traversal)
中序遍历是先访问左节点,再访问根节点,最后访问右节点。
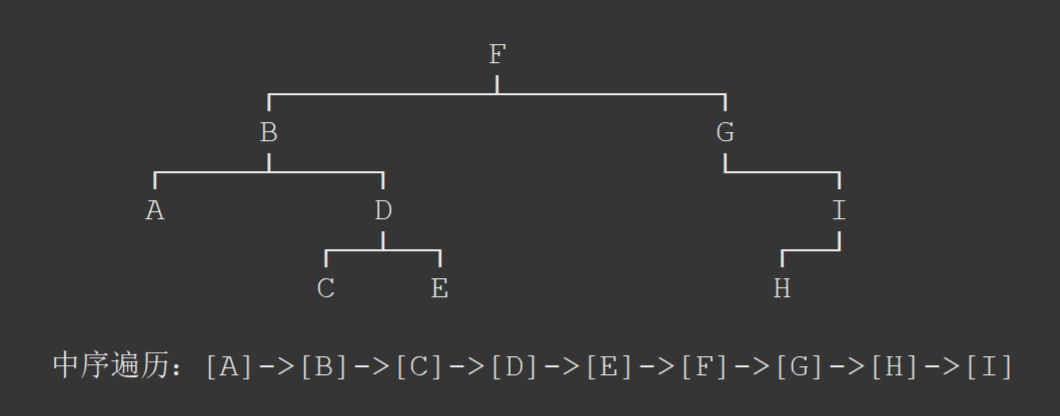
以上图为例:
- (1)从根节点 F 开始,按照中序遍历的规则,首先遍历F的左子树B。
- 遍历B的左子树A
- 遍历A的左子树,为空,跳过。
- 遍历A的根节点,输出A。
- 遍历A的右子树,为空,跳过。
- 遍历B的根节点,输出B。
- 遍历B的右子树D
- 遍历D的左子树C
- 遍历C的左子树,为空,跳过。
- 遍历C的根节点,输出C。
- 遍历C的右子树,为空,跳过。
- 遍历D的根节点,输出D。
- 遍历D的右子树E
- 遍历E的左子树,为空,跳过。
- 遍历E的根节点,输出E。
- 遍历E的右子树,为空,跳过。
- (2)现在根节点 F 的左子树遍历完了,接着遍历F的根节点,输出F
- (3)最后遍历F的右子树G
- 遍历G的左子树,为空,跳过。
- 遍历G的根节点,输出G。
- 遍历G的右子树I
- 遍历I的左子树H。
- 遍历H的左子树,为空,跳过。
- 遍历H的根节点,输出H。
- 遍历H的右子树,为空,跳过。
- 遍历I的根节点,输出I。
- 遍历I的右子树,为空,跳过。
遍历逻辑写的很清楚了,因此,中序遍历的顺序为 [A]->[B]->[C]->[D]->[E]->[F]->[G]->[H]->[I]。
实际上,上图二叉树是一个二叉搜索树。我们发现,对于二叉搜索树来讲,中序遍历后的结果是升序的。这很有意思。由于在二叉搜索树中,左子树的值小于根节点的值,右子树的值大于根节点的值。所以结果是显而易见的。如果我们先访问右子树,再访问根结点,最后访问左子树,此时遍历的结果是降序的。
中序遍历实际上就是将根节点放在左子树和右子树的中间进行遍历,不一定非要先访问左子树,也可以先访问右子树,然后访问根节点,最后访问左子树。
- Q:先访问右子树,然后访问根节点,最后访问左子树,也是中序遍历嘛?
- A:二叉树的遍历实际上是一种基于根节点的划分,将根节点放在左右子树的中间进行遍历就算是中序遍历,因此不一定非要先访问左子树,也可以先访问右子树,然后访问根节点,最后访问左子树,根据我们的具体需求。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
inorder(root, result);
return result;
}
public void inorder(TreeNode node, List<Integer> result) {
if (node == null) {
return;
}
inorder(node.left, result);
result.add(node.val);
inorder(node.right, result);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop();
result.add(cur.val);
cur = cur.right;
}
}
return result;
}
|
后序遍历(Post-Order Traversal)
看完前两个遍历,我们也能猜出后序遍历的规则了。
没错,后序遍历的遍历顺序为左子树、右子树、根节点。具体来说,在后序遍历中,我们先遍历左子树,然后遍历右子树,最后访问根节点。
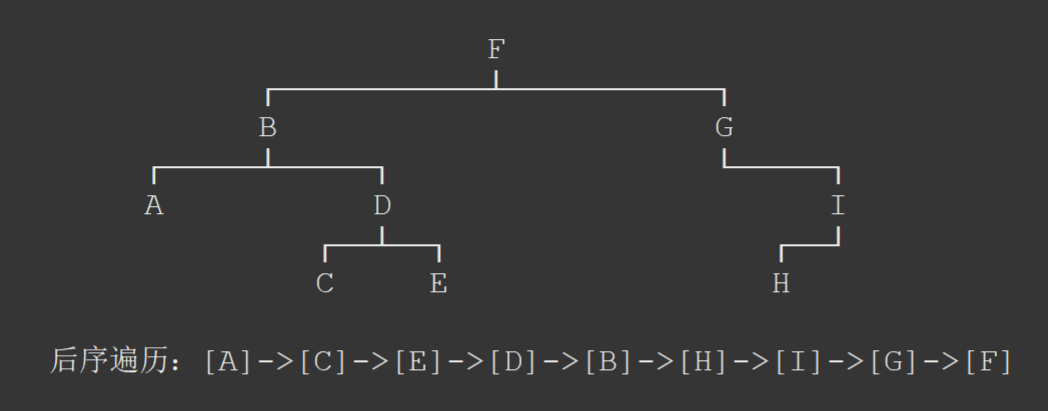
以上图为例:
- (1)从根节点 F 开始,按照后序遍历的规则,首先遍历F的左子树B。
- 遍历B的左子树A
- 遍历A的左子树,为空,跳过。
- 遍历A的右子树,为空,跳过。
- 遍历A的根节点,输出A。
- 遍历B的右子树D
- 遍历D的左子树C
- 遍历C的左子树,为空,跳过。
- 遍历C的右子树,为空,跳过。
- 遍历C的根节点,输出C。
- 遍历D的右子树E
- 遍历E的左子树,为空,跳过。
- 遍历E的右子树,为空,跳过。
- 遍历E的根节点,输出E。
- 遍历D的根节点,输出D。
- 遍历B的根节点,输出B。
- 现在根节点 F 的左子树遍历完了,接着遍历F的右子树G
- 遍历G的左子树,为空,跳过。
- 遍历G的右子树I
- 遍历I的左子树H。
- 遍历H的左子树,为空,跳过。
- 遍历H的右子树,为空,跳过。
- 遍历H的根节点,输出H。
- 遍历I的右子树,为空,跳过。
- 遍历I的根节点,输出I。
- 遍历G的根节点,输出G。
- 现在根节点 F 的左右子树都遍历完了,最后再遍历F的根节点,输出F。
因此,后序遍历的顺序为 [A]->[C]->[E]->[D]->[B]->[H]->[I]->[G]->[F]。
代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
postorder(root, result);
return result;
}
public void postorder(TreeNode node, List<Integer> result) {
if (node == null) {
return;
}
postorder(node.left, result);
postorder(node.right, result);
result.add(node.val);
}
|
这里用到一个小技巧。和先序遍历类似,我们先访问根节点,然后遍历右子树,最后遍历左子树,此时遍历的顺序是根右左,因此我们将result反转后就得到了后序遍历的结果数组,即遍历顺序是左右根。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
result.add(node.val);
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
}
Collections.reverse(result);
return result;
}
|
小结 | 前中后序遍历

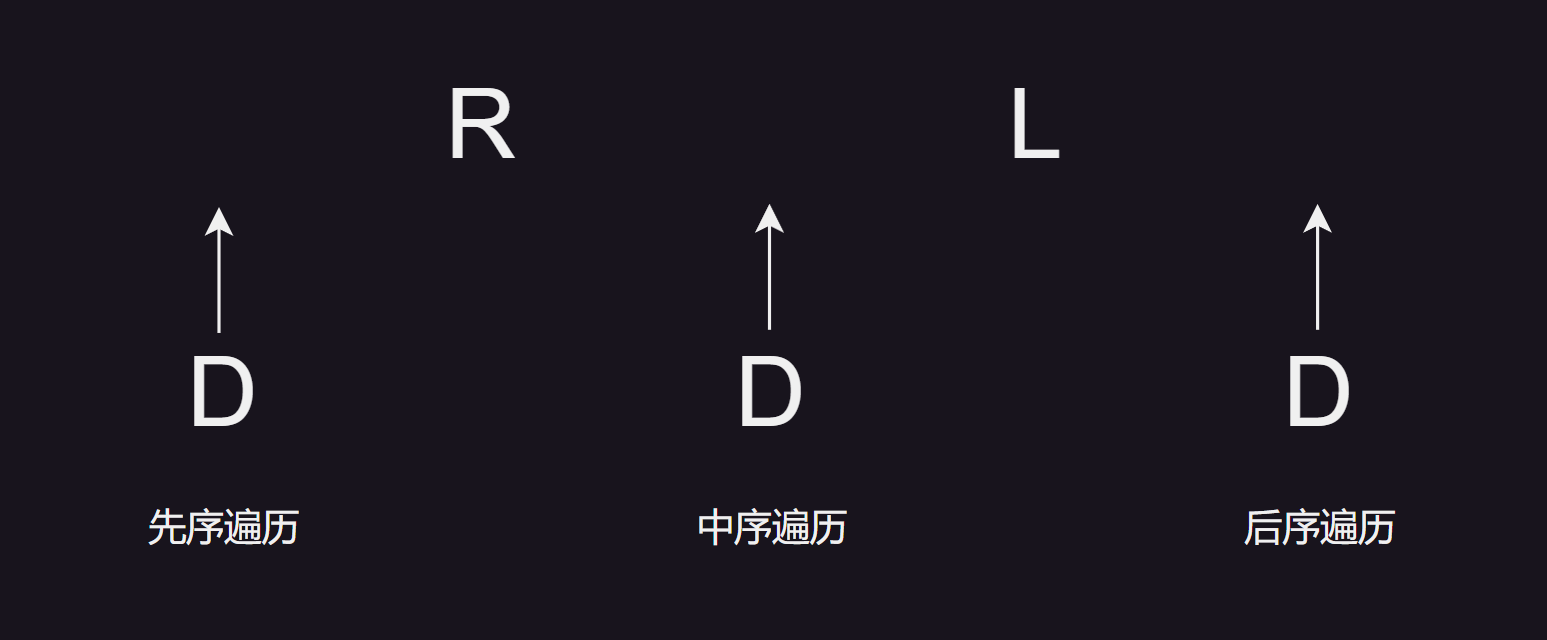
让我们用 L、D、R 分别表示遍历左子树、访问根节点和遍历右子树。
那么:
D L R:先序遍历二叉树的顺序(或者D R L)L D R:中序遍历二叉树的顺序(或者R D L)L R D:后序遍历二叉树的顺序(或者R L D)
备注:我们主要观察访问根节点的访问时机,就可以判断属于哪种遍历。
层序遍历(Level Order Traversal)
最后是层序遍历。
层序遍历,就是从上到下,从左到右依次访问每一个节点。
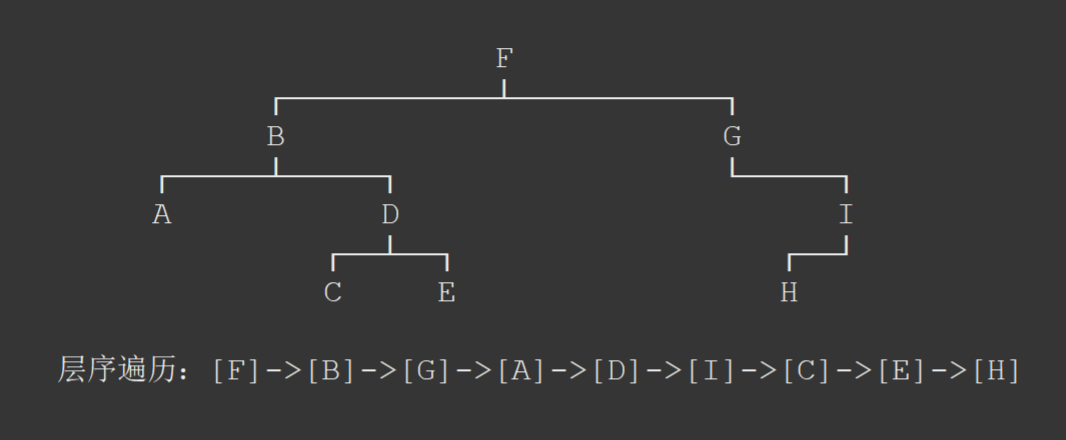
如上图所示。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
public List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> levelOrderTraversal(TreeNode root) {
levelOrder(root, 0);
return result;
}
public void levelOrder(TreeNode node, Integer level) {
if (node == null) return;
if (result.size() <= level) {
List<Integer> item = new ArrayList<Integer>();
result.add(item);
}
result.get(level).add(node.val);
levelOrder(node.left, level + 1);
levelOrder(node.right, level + 1);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
public List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> levelOrderTraversal(TreeNode root) {
levelOrder(root);
return result;
}
public void levelOrder(TreeNode node) {
if (node == null) return;
Queue<TreeNode> que = new LinkedList<>();
que.offer(node);
while (!que.isEmpty()) {
List<Integer> itemList = new ArrayList<>();
int len = que.size();
while (len > 0) {
TreeNode tmpNode = que.poll();
itemList.add(tmpNode.val);
if (tmpNode.left != null) que.offer(tmpNode.left);
if (tmpNode.right != null) que.offer(tmpNode.right);
len--;
}
result.add(itemList);
}
}
|
复习巩固










